

Over the surface, we must express it in terms of the parameters and insert the result as a factor in the integrand. This is going to be too complicated to integrate symbolically, so we do a numerical integration, using the numerical integrationĪrea=newnumint2(surffactor,p,0,pi,t,0,2*pi) Surffactor = simple(veclength(cross(diff(ellipsoid,t). Now we compute the surface area factor: realdot = u*transpose(v) To check that this really is a parametrization, we verify the original equation: simplify(subs((x^2/4)+(y^2/9)+z^2,ellipsoid))Īnd we can also draw a picture with ezsurf:Įzsurf(ellipsoid(1),ellipsoid(2),ellipsoid(3),) We may parametrize this ellipsoid as we have done in the past, using modified spherical coordinates: syms x y z p tĮllipsoid=

To see how this works, let us compute the surface area of the ellipsoid whose equation is Which enables us to compute the area of a parametrized surface, or to integrate any function along the surface with respect Taking lengths on both sides of the above formula above gives The key idea behind all the computations is summarized in the formulaĪre vectors, and their cross-product is a vector with two important properties: it is normal to the surface parametrizedīy P, and its length gives the scale factor between area in the parameter space and the corresponding area on the surface. In other words, the surface is given by a vector-valued function P (encoding the x, y, and z coordinates of points on the surface) depending on two parameters, say u and v. Recall that a surface is an object in 3-dimensional space Please join us in the ACM users Google Group to make any suggestions for corrections or improvements, as well as get updates on other elements of our work.In this lesson, we will study integrals over parametrized surfaces.
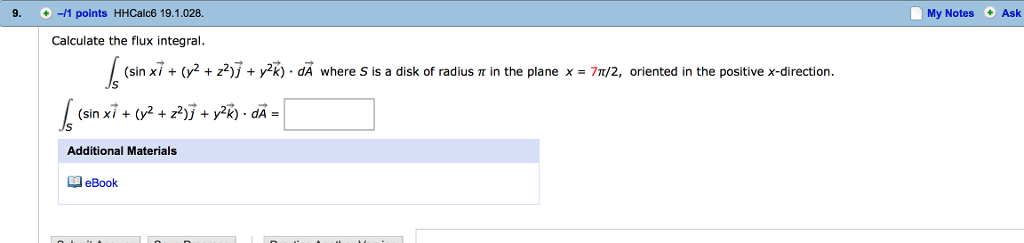
CALCULATE FLUX INTEGRAL 3D MANUAL
Over the next couple of years, Mitch and I will be working on edits to other parts of ACM including creating a solutions manual and updating other elements across ACM for consistency and easy of use (for students and faculty).

(ACM’s Preview Activities are not yet implemented using WeBWorK, but the WeBWorK exercises at the ends of sections can be assigned in Runestone.)
CALCULATE FLUX INTEGRAL 3D UPDATE
As Matt included in his update post, you should check out all of the amazing features that come with hosting materials on Runestone. For instance, line integrals of vector fields use the notation \(\int_C\vec\) to emphasize that we are looking at the accumulation (integral) of the dot product of our vector field with displacement.ĪCM (as well as ACS) is now available on Runestone as well. We selected notations for vector calculus that emphasize the nature of what we are measuring and make notes or comments about other notations that students will see in other sources. In order to aid faculty in planning how they will use Chapter 12, we also have given a flow chart of dependencies for the twelve sections in vector calculus. Since vector calculus is a set of topics that has quite a variety coverage levels at institutions, we tried to make it possible to do surface level coverage or deeper discovery-based activities. Many of these are rooted in physical measurements but the descriptions do not assume any physics background. The motivation and presentation of topics in Chapter 12 has been approached from the perspective of trying to measure a particular quantity, like the amount of vector field that flows through a surface or work done by a vector field while moving along a path. In the summer 2023 edits, we have added WeBWorK and pencil and paper exercises to each of the twelve sections in Chapter 12. Chapter 12 also includes the frequent use of Sage interactive elements when displaying graphics of math elements in 3D. While the previous versions of this material were rough in spots and sometimes were not parsed into pieces that were right for in class activities, our new presentation has been simplified and activities are more consistent in length and effort levels. We have incorporated a lot of the feedback and made significant revisions to the materials on vector calculus which will now be included as Chapter 12 of ACM. A few years ago, we started writing material for a chapter on vector calculus topics which many of you have tried and tested.
In case you hadn’t heard already, Steve Schlicker is retiring soon (Congrats!) and we have taken over managing and editing Active Calculus – Multivariable (ACM).


 0 kommentar(er)
0 kommentar(er)
